Descriptors

For two-phase morphology, current py-graspi computes the following descriptors: We refer to graph-centric terms defined in basic definitions section.

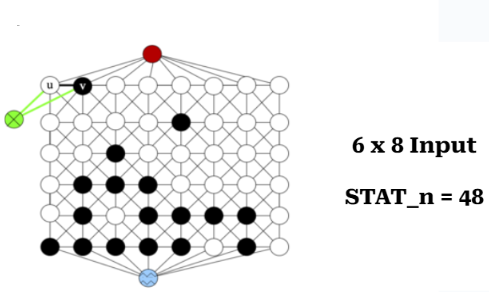
STAT_n

STAT_n is number of vertices excluding meta ones in the morphology. It is the total number of vertices in the graph. It simply the cardinality of set \(V\).

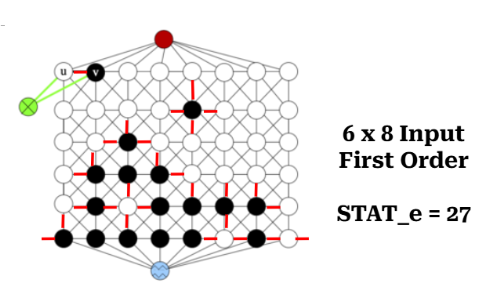
STAT_e

STAT_e is the number of interface edges. It is the interfacial area, this is the total number of edges in the graph connecting BLACK and WHITE vertices. Three steps are involved:

1. Input: Given labeled, weighted, undirected graph \(G=(V,E,W,L,L_e)`\).

2. Construct set of edges, \(I=\{e=(u,v)\in E\;|\; (L_e(e)=f)\;\land\; ( L(u)=BLACK \land L(v)=WHITE\}\).

3. Output: \(|I|\) – the cardinality of interface edges.

   

STAT_n_D

STAT_n_D - number of black vertices

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Identify set \(B\) of all (electron donor) black vertices.

3. Output: \(|B|`\), where \(|.|`\) is the cardinality of the set.

STAT_n_A

STAT_n_A - number of white vertices

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Identify set \(W\) of all (electron donor) black vertices.

3. Output: \(|W|\), where \(|.|`\) is the cardinality of the set.

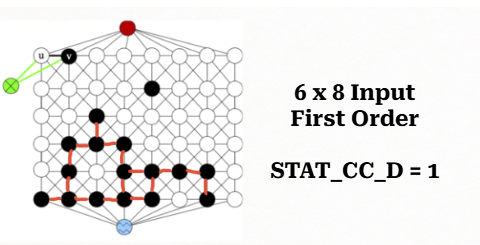
STAT_CC_D

STAT_CC_D - number of black connected components

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct vertex-induced subgraph, \(G'=(V',E')\), where \(V'=\{v \in V\}\) is a set of all BLACK vertices in \(V\), \(E'`\) is a set of all edges between vertices in \(V'\).

3. Compute the set of connected components, \(C_B\), in \(G'\).

4. Output: \(|C_B|\).

   

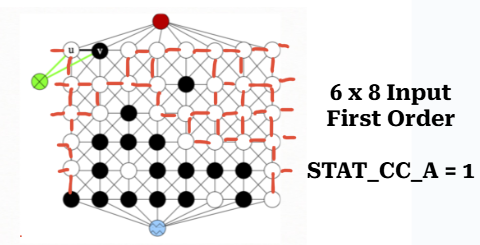
STAT_CC_A

STAT_CC_A - number of white connected components

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct vertex-induced subgraph, \(G'=(V',E')\), where \(V'=\{v \in V\}\) is a set of all WHITE vertices in \(V\), \(E'`\) is a set of all edges between vertices in \(V'\).

3. Compute the set of connected components, \(C_W\), in \(G'\).

4. Output: \(|C_W|\).

   

STAT_CC_D_An

STAT_CC_D_An - number of black connected components connected to top (red)

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Reconstruct the neighborhood of RED vertex \(ngbr_R\) in \(G\).

3. Construct vertex-induced subgraph, \(G'=(V',E')\), where \(V'=\{v \in V\}\) is a set of all BLACK vertices in \(V\), \(E'`\) is a set of all edges between vertices in \(V'\).

4. Compute the set of connected components, \(C_B\), in \(G'\).

5. Compute the set \(C_B^R\) of indices of connected components in \(ngbr_R\) using the set \(C_B\).

6. Output: \(|C_B^R|\).

STAT_CC_A_Ca

STAT_CC_A_Ca - number of white connected components connected to bottom (blue)

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Reconstruct the neighborhood of BLUE vertex \(ngbr_B\) in \(G\).

3. Construct vertex-induced subgraph, \(G'=(V',E')\), where \(V'=\{v \in V\}\) is a set of all WHITE vertices in \(V\), \(E'`\) is a set of all edges between vertices in \(V'\).

4. Compute the set of connected components, \(C_W\), in \(G'\).

5. Compute the set \(C_W^B\) of indices of connected components in \(ngbr_B\) using the set \(C_W\).

6. Output: \(|C_W^B|\).

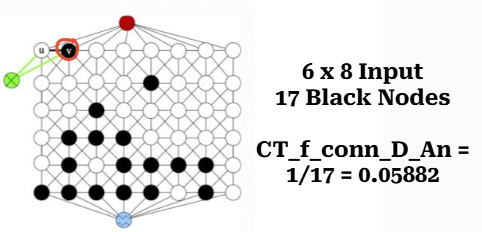
CT_f_conn_D_An

CT_f_conn_D_An - fraction of black vertices connected to top

We use the same steps as in STAT_CC_D_An. With one more step:

6. Let \(P\) be the union of all BLACK vertices in \(C_B^R\).

7. Output: \(|P|/|B|\), where \(B\) is the set of BLACK vertices.

   

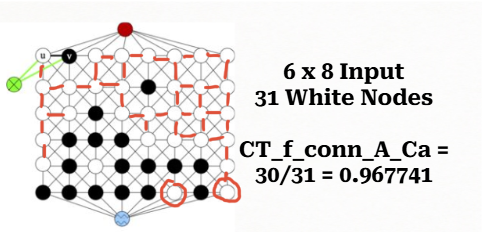
CT_f_conn_A_Ca

CT_f_conn_A_Ca - fraction of white vertices connected to bottom

We use the same steps as in STAT_CC_D_An. With one more step:

6. Let \(P\) be the union of all WHITE vertices in \(C_W^B\).

7. Output: \(|P|/|B|\), where \(W\) is the set of WHITE vertices.

   

ABS_f_D

ABS_f_D - fraction of black vertices

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Identify set \(B\) of all BLACK vertices.

3. Output: \(|B|/|V|`\), where \(|.|`\) is the cardinality of the set.

ABS_wf_D

ABS_wf_D - weighted fraction of black vertices

DISS_f10_D

DISS_f10_D - fraction of black vertices in 10 distance to interface

This descriptor is constructed in three steps. First, we construct the subgraph induced by a set of BLACK and GREEN vertices. Next, using Dijkstra’s algorithm the shortest paths between GREEN vertex and all other vertices in the induced subgraph are determined. The distance is weighted by the physics-informed function (here: \(f(d)=exp(-d/L_d)\), where \(L_d\) is the exciton diffusion length). Formally:

1. Input: Given labeled, weighted, undirected graph \(G=(V,E,W,L)\).

2. Construct vertex-induced subgraph, \(G'=(V',E')`\), where: \(V'`\) is a set of all BLACK and GREEN vertices in \(V\), \(E'\) is a set of all edges between vertices in \(V'`\).

3. Find all shortest paths in \(G'\) from GREEN vertex \(u' :math:`(L(u) = GREEN)\).

4. Identify vertex set \(V_d=\{v \in V'\;|\;\) (shortest_path(\(v\)) \(<d\)) \(\land (L(v) = BLACK)\}\). Shortest_path (\(v\)) denotes the distance between \(u\) and \(v\) in \(G'`\).

5. Weight each distance \(d\) with the weighting function (\(f(d)=exp(-d/L_d)\)).

6. Output: \(\sum_{i=1..|B|} f(d)i)/|B|`\), where \(|B|\) is the cardinality of a set that consists of BLACK vertices.

CT_f_e_conn

CT_f_e_conn - fraction of interface with complementary paths to bottom and top

We search for interface edges in the graph that connect BLACK and WHITE vertices (interface), where both vertices have paths to relevant electrodes (BLACK vertex has path to RED meta-vertex and WHITE vertex has path to BLUE meta-vertex). Formally,

• Let \(G_B\) be the vertex-induced subgraph with BLACK and RED vertices.

• Let \(G_W\) be the vertex-induced subgraph with WHITE and BLUE vertices.

• Find a set \(I_c\subset I\) of interface edges in the graph, such that the path from the BLACK vertex to RED exists in \(G_B\) and the path from WHITE vertex to BLUE exists in \(G_W\).

This is computed using the following algorithm:

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct a filtered graph, \(G'=(V,E')`\), where \(E'`\) is a set of edges connecting vertices of the same color.

3. Let \(I\) be the set of all interface edges.

4. Identify connected components, \(C\), in \(G'\).

5. Compute subset \(R_r \subset C\) of all components \(c\in C\), such that \(c\) has BLACK vertices adjacent to RED in \(G\) (from CT_f_conn_D_An).

6. Compute subset \(R_b \subset C\) of all components \(c\in C\), such that \(c\) has WHITE vertices adjacent to BLUE in \(G\) (from CT_f_conn_A_Ca).

7. Identify subset, \(I_{rb} \subset I\) where BLACK vertex belongs to set of vertices in \(R_r\) and WHITE vertex belongs to set of vertices in \(R_b\).

8. Output: \(|I_{rb}|/|I|\).

This descriptor is formulated in a hierarchical way using CT_f_conn_D_An and CT_f_conn_A_Ca. This hierarchical construction is one additional advantage of our graph-based approach. Moreover, the next descriptor is computed using intermediate data from this descriptor.

CT_e_conn

CT_e_conn - number of interface edges with complementary paths

This descriptor is computed as an intermediate step in the algorithm from CT_f_e_conn. The number of interface edges is the cardinality of the set \(|I_{rb}|\).

CT_e_D_An

CT_e_D_An - number of black interface vertices with path to top

This descriptor is computed as an analogous way as CT_f_e_conn.

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct a filtered graph, \(G'=(V,E')`\), where \(E'`\) is a set of edges connecting vertices of the same color.

3. Let \(I\) be the set of all interface edges.

4. Identify connected components, \(C\), in \(G'\).

5. Compute subset \(R_r \subset C\) of all components \(c\in C\), such that \(c\) has BLACK vertices adjacent to RED in \(G\) (from CT_f_conn_D_An).

6. Compute subset \(R_b \subset C\) of all components \(c\in C\), such that \(c\) has WHITE vertices adjacent to BLUE in \(G\) (from CT_f_conn_A_Ca).

7. Identify subset, \(I_{r} \subset I\) where BLACK vertex belongs to set of vertices in \(R_r\).

8. Output: \(|I_{r}|\).

CT_e_A_Ca

CT_e_A_Ca - number of white interface vertices with path to bottom

This descriptor is computed as an analogous way as CT_f_e_conn.

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct a filtered graph, \(G'=(V,E')`\), where \(E'`\) is a set of edges connecting vertices of the same color.

3. Let \(I\) be the set of all interface edges.

4. Identify connected components, \(C\), in \(G'\).

5. Compute subset \(R_r \subset C\) of all components \(c\in C\), such that \(c\) has BLACK vertices adjacent to RED in \(G\) (from CT_f_conn_D_An).

6. Compute subset \(R_b \subset C\) of all components \(c\in C\), such that \(c\) has WHITE vertices adjacent to BLUE in \(G\) (from CT_f_conn_A_Ca).

7. Identify subset, \(I_{b} \subset I\) where WHITE vertex belongs to set of vertices in \(R_b\).

8. Output: \(|I_{b}|\).

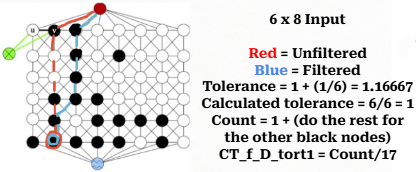
CT_f_D_tort1

CT_f_D_tort1 - fraction of black vertices with straight rising paths (t=1)

Straight rising paths are paths with tortuosity one (\(t\)). Tortuosity is the ratio between the path length to the relevant electrode through morphology, and ideal straight path length to the electrode without any constraints. Tortuosity is computed for domains that are connected to relevant electrode. In case of this descriptor, the donor domains (BLACK vertices) connected to top boundary (RED meta-vertex) are considered.

The graph-based algorithm to compute the fraction is given below:

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct vertex-induced graph, \(G'=(V',E')\), where \(V'=\{v \in V\}\) is a set of all BLACK and RED vertices in \(V\), \(E'\) is a set of all edges between vertices in \(V'\).

3. Let \(V_B\subset V'\) be a set of BLACK vertices in \(V'\) in \(G\).

4. Find the shortest paths from the RED to all BLACK vertices in \(G'\) (filtered graph - step 2).

5. Find the shortest paths from the RED to all BLACK vertices in \(G\) (original graph).

6. For each BLACK vertex compute the tortuosity using the shortest paths from step 5 and 4.

7. Filter the set \(V_{Bt1}\) with all BLACK vertices that have the shortest path with \(t=1\).

8. Output: The fraction of BLACK vertices with straight rising paths \(|V_{Bt1}|/|V_B|\).

   

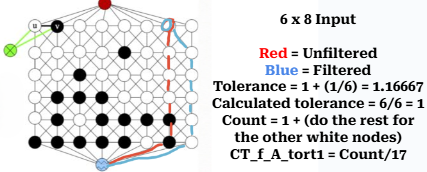
CT_f_A_tort1

CT_f_A_tort1 - fraction of white vertices with straight rising paths (t=1)

Similar to previous descriptor, the acceptor domains (WHITE vertices) connected to bottom boundary (BLUE meta-vertex) are considered.

The graph-based algorithm to compute the fraction is given below:

1. Input: Given labeled, weighted, undirected graph, \(G=(V,E,W,L)\).

2. Construct vertex-induced graph, \(G'=(V',E')\), where \(V'=\{v \in V\}\) is a set of all WHITE and BLUE vertices in \(V\), \(E'\) is a set of all edges between vertices in \(V'\).

3. Let \(V_W\subset V'\) be a set of WHITE vertices in \(V'\) in \(G\).

4. Find the shortest paths from the BLUE to all WHITE vertices in \(G'\) (filtered graph - step 2).

5. Find the shortest paths from the BLUE to all WHITE vertices in \(G\) (original graph).

6. For each WHITE vertex compute the tortuosity using the shortest paths from step 5 and 4.

7. Filter the set \(V_{Wt1}\) with all WHITE vertices that have the shortest path with \(t=1\).

8. Output: The fraction of WHITE vertices with straight rising paths \(|V_{Wt1}|/|V_W|\) .

   

CT_n_D_adj_An

CT_n_D_adj_An - number of black vertices in direct contact with top (An - top/anode)

This descriptor computes the number of BLACK vertices with distance to RED (Anode/top) vertex. To compute this descriptor, post processing of distance vector is performed. By counting the number of BLACK vertices with zero distance to the RED vertex.

CT_n_A_adj_Ca

CT_n_A_adj_Ca - number of white vertices in direct contact with bottom (Ca - bottom/cathode)

This descriptor computes the number of WHITE vertices with distance to BLUE (Cathode/bottom) vertex. To compute this descriptor, post processing of distance vector is performed. By counting the number of WHITE vertices with zero distance to the BLUE vertex.